5.1.- R: Control de proceso, valoración estadística de una variable ....

 Una de las aplicaciones prácticas de la estadística univariante es el control de estadístico de proceso, vamos a ver cómo se puede realizar en R. Para facilitar el seguimiento del código no usaré variables, en un entorno profesional o de programación lo estándar seria almacenar valores en variables y después usarlos (el operador de asignación en R es:  '<-'), de esa forma evitamos que R tenga que cálcular continuamente valores.

 Resumiendo mucho, sabemos que un proceso está bajo control estadístico cuando sigue una distribución normal, centrada en las tolerancias, su indice de capacidad Cpk>1,33 ... hay abundante literatura disponible al respecto. 

 Por motivos de disponibilidad de datos, para esta entrada del blog usaremos los datos disponibles en R/RStudio. Cómo hemos indicado anteriormente muchos de los paquetes de R vienen con conjuntos de datos disponibles para poder utilizar. En la captura de pantalla a continuación vemos en la pestaña "Packages" los paquetes  que tenemos disponibles, y tecleando data(), se nos abre la pestaña "R data sets" que nos muestra los data sets que tenemos activos:

Para nuestro caso vamos a cargar los datos del nivel del Lago Huron como si fuera un proceso  y extraeremos las medidas de centralización y dispersión :

hemos usado dos nuevas instrucciones de R :

• paste (...) para unir dos cadenas de caracteres, R convierte a cadena de texto la salida numérica de las funciones.
• format(...) para formatear la salida numérica al número de dígitos que deseemos.

 Podemos ver cómo en el entorno global está disponible la variable LakeHuron y cómo por consola se han producido las salida de la función paste(...). Para no complicar innecesariamente esta entrada, no utilizaremos una salida Markdown (ver entrada en este blog 4.1).

 Hemos caracterizado numéricamente la distribución de nuestros datos, y ahora completaremos la caracterización con un análisis gráfico.

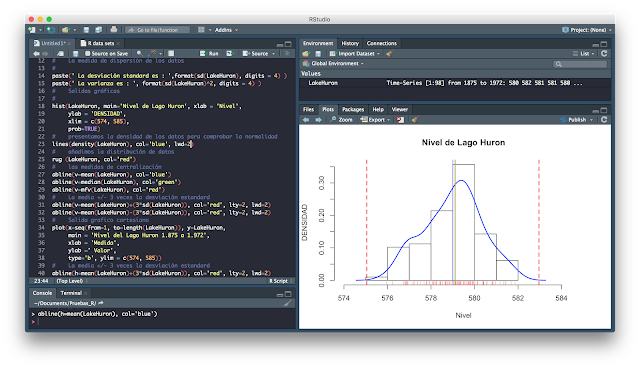
 En primero lugar sacaremos el histograma de la distribución de datos, como vemos a continuación :

Hemos utilizado una nueva instrucción :

• rug(...) Nos permite de forma aproximada ver dónde se acumula la mayor cantidad de valores, para hacernos una idea del tipo de distribución que tenemos.

sobre este histograma, con la instrucción abline(...) representaremos a continuación :

• la media : color azul
• la mediana : color verde
• la moda : color rojo

gráficamente podemos ver que hay una diferencia entre los tres valores de centralización, la moda el valor que más se repite, la mediana el valor que centra la distribución y la media el valor calculado entre todos los valores. Nosotros debemos tomar la decisión de que hacer con esta diferencia, ¿los dos valores que hay entorno a 576 que lastran el valor de la media a un lado,  son significativos, debemos tenerlos en cuenta?

 Finalmente para completar el estudio de capacidad, si el nivel del Lago Huron fuera un proceso, añadiremos dos valores más que son la media y 3 veces la desviación estándar en cada dirección :

 Para poder representar ambos valores, he tenido que modificar la escala del histograma añadiendo el parámetro xlim=(...), como la concatenación de dos valores.

 Hasta ahora hemos presentado los datos de nuestra distribución de valores, pretendemos que los datos del nivel del lago que representan un proceso, y lo hemos presentado por si mismos, respecto a sus medidas de centralización y dispersión. Para terminar el estudio de la capacidad del proceso faltaría añadir la posición de las tolerancias del nivel del lago, mediante la instrucción abline(...) y realizando los cálculos necesarios calcular los correspondientes indices de capacidad.

 Un histograma no nos permite ver patrones en el comportamiento de los datos, si la recogida de los datos ha sido cronológica podemos representarlo en un gráfico cartesiano como vemos a continuación :

 Este gráfico nos permite apreciar en el nivel del lago la tendencia en el tiempo, patrones en el comportamiento, ...

 Para este gráfico tipo cartesiano,  no necesitamos más que cambiar respecto al histograma anterior en abline(...), la v ( de vertical ) por h ( de horizontal) y ajustar los limites de la variable y de plot(...) con el parámetro ylim. Hemos de tener en cuenta que los valores del eje x (seq(from=1, to=....))  como hemos hecho en otras entradas, es una secuencia desde 1 hasta la longitud (el numero de valores) en la variable LakeHuron.

Hemos visto como con un conjunto de instrucciones muy sencillas es posible caracterizar completamente nuestra distribución de datos y su posición respecto a unas tolerancias (en nuestro caso por razones obvias no las hemos usado) y a partir de ahí se pueden tomar decisiones informadas al respecto del proceso. 

 Finalmente, en relación al control estadístico de procesos no quisiera terminar sin añadir dos puntos más :

• La comprobación de normalidad de la distribución de los datos.
• El muestreo de datos.

 R nos permite comprobar la distribución de normalidad de los datos gráficamente mediante la instrucción density(...), como vemos a continuación en nuestro código modificado :

 Hemos añadido al código la función R lines(...) y modificado en el hist(...) añadiendo  el parámetro prob=TRUE, para que no cuente el histograma frecuencia sino probabilidad.

 Podemos comprobar de forma numérica la normalidad de la distribución de los datos, ver enlaces abajo, entre otros con un contraste de hipótesis  Shapiro-Wilk 

¿ por que es necesario comprobar la normalidad de la distribución de los datos ? como hemos dicho anteriormente es muy difícil de una muestra de datos extraer conclusiones para una población, una distribución de datos normal está completamente caracterizada y sabemos que entre su media y +/-3 veces la desviación estándar está el 99% de la población, por tanto la comprobación de normalidad es un requisito indispensable antes de avanzar en el control estadístico de procesos.

 Expresamos el indice de capacidad del proceso Cpk posicionando el 99% de los datos, normalmente suele ser una muestra y no un a población, respecto a las tolerancias del proceso.

 Finalmente aunque se escapa de lo que es programar R no quiero deja sin hablar del muestreo, hemos de tener en cuenta que excepto que controlemos el 100% de la población; el teorema del limite central nos dice que si muestreo a cantidad constante una población determinada, obtendremos una distribución de datos de la muestra normal con la misma media que la población original. Estaremos viendo en nuestro análisis una muestra con distribución normal, pero de ahí no se puede extraer la consecuencia de que la población sea normalmente distribuida.

 La desviación estándar de la población es la desviación estándar de la muestra (se llama error estándar)  multiplicada por la raíz cuadrada del tamaño de la muestra, en determinados casos eso puede dar al traste con muchos procesos ....

Para una introducción al control estadístico de procesos ver : Link

Para un estudio sobre la capacidad de procesos ver : Link

Para la comprobación de normalidad ver : Link